The Advanced Photon Source
a U.S. Department of Energy Office of Science User Facility

X-Ray Server: BRL, GID_sl, TER_sl, TRDS_sl, MAG_sl, and X0h

 

X-ray Server was launched in 1997 with the goal to provide wide scientific community with access to personal research results and for refining X-ray scattering models and scientific software via WWW technologies.  The Server delivers a number of programs implementing author’s models in the field of X-ray diffraction and scattering. Since computations are provided via a Web interface, there is no need to download, compile or install code. Recent developments offer remote access to the Server programs from user-written software rather than restricting access to be via a web browser. This  converts the Server into a new class of software library, where a computational toolkit is available for remote access and even allows for remote data fitting.Currently, seven programs have been made operational:
  • X0h calculates scattering amplitudes for crystals.
  • X0h_search searches for Bragg planes in crystals under various conditions.
  • GID_sl calculates X-ray Bragg diffraction rocking curves from perfect, strained and multilayered crystals, accounting for interface roughness.
  • TER_sl calculates X-ray specular reflection and respective X-ray standing waves from X-ray mirrors and multilayers allowing for interface roughness or transition layers.
  • TRDS_sl calculates non-specular X-ray scattering from multilayers due to interface roughness.
  • MAG_sl calculates resonant X-ray specular reflection from magnetic multilayers taking into account interface roughness or transition layers.
  • BRL calculates multiple Bragg diffraction of X-rays from crystals including cases with X-ray waves grazing along the crystal surface and with Bragg angles close to 90 degrees.

Further information on each program is provided in the Details Section.

 

Distribution & Impact

The X-Ray Server programs are accessed via WWW using web browsers or can be embedded into workflows using scripts (sample scripts are provided) without any installation on the user side or need for registration.  The scripted access is offered for massive calculations (e.g. data fitting) and for embedding the Server calls into a user’s software as would be done with an installable software library.The server programs have been used close to 2,000,000 times since their launch in 1997.The distribution of usage among different programs is provided on the homepage.  The majority of users come from synchrotron radiation facilities and universities around the globe.Approximately 6,000 users access the code on a regular basis, as noted from IP addresses where more than 10 job requests have been submitted.

 

Funding Source

X-Ray Server hosting is provided by GMCA@APS, which is funded by the National Institute of General Medical Sciences (NIGMS) and National Cancer Institute (NCI) of the National Institutes of Health (NIH).

 

Please cite

S. Stepanov, "X-ray server: an online resource for simulations of X-ray diffraction and scattering", in: "Advances in Computational Methods for X-ray and Neutron Optics", Ed. M. Sanches del Rio; Proceedings SPIE, 5536, 16-26, (2004).
Related Publications
  1. S. Stepanov,"Transformation of X-ray Server from a set of WWW-accessed programs into WWW-based library for remote calls from X-ray data analysis software", Thin Solid films, 515, 5700-5703, (2007).
  2. S. Stepanov and R. Forrest,"Fitting dynamical X-ray diffraction data over the World Wide Web",J. Appl. Cryst., 41, 958-962, (2008).
  3. O.M. Lugovskaya and S.A. Stepanov,"Calculation of the polarizabilities of crystals for diffraction of X-rays of the continuous spectrum at wavelengths of 0.1-10 A",Sov. Phys. Crystallogr. 36, 478-481, (1991).
  4. S.A. Stepanov, U. Pietsch and G.T. Baumbach,"A matrix approach to X-ray grazing-incidence diffraction in multilayers",Zeitschrift für Physik B, 96, 341-347, (1995).
  5. S.A. Stepanov and R. Koehler,  "Real-structure effects in the dynamical theory of grazing incidence X-ray diffraction",J. Appl. Phys. 76, 7809-7815, (1994).
  6. S.A. Stepanov and R. Koehler,"A dynamical theory of extremely asymmetric X-ray diffraction taking account of normal lattice strain",J. Phys. D: Applied Physics, 27, 1923-1928, (1994).
  7. S.A. Stepanov, E.A. Kondrashkina, R. Koehler, D.V. Novikov, G. Materlik, and S.M. Durbin,"Dynamical X-ray diffraction of multilayers and superlattices: Recursion matrix extension to grazing angles",Phys. Rev. B, 57, 4829-4841, (1998).
  8. V.M. Kaganer, S.A. Stepanov and R. Koehler,"Bragg-diffraction peaks in X-ray diffuse scattering from multilayers with rough interfaces,"Phys. Rev. B, 52, 16369-16372, (1995).
  9. E.A. Kondrashkina, S.A. Stepanov, R. Opitz, M. Schmidbauer, R. Koehler, R. Hey, M. Wassermeier, and D.V. Novikov,"Grazing-incidence X-ray scattering from stepped interfaces in AlAs/GaAs superlattices",Phys. Rev. B, 56, 10469-10482, (1997).
  10. S.A. Stepanov and S.K. Sinha,"X-ray resonant reflection from magnetic multilayers: Recursion matrix algorithm",Phys. Rev. B, 61, 15302-15311, (2000).
  11. D.R. Lee, S.K. Sinha, D. Haskel, Y. Choi, J.C. Lang, S.A. Stepanov, and G. Srajer,"X-ray resonant magnetic scattering from structurally and magnetically rough interfaces in multilayered systems. I. Specular reflectivity",Phys. Rev. B, 68, 224409, (2003).
  12. S.A. Stepanov and A.P. Ulyanenkov,"A new algorithm for computation of X-ray multiple Bragg diffraction",Acta Cryst., A50, 579-585, (1994).
  13. M. Grundmann and A. Krost"Atomic structure based simulation of X-Ray scattering from strained superlattices",  Phys. Status Solidi. (b), 218, 417–423, (2000).
  14. S.K. Sinha, E.B. Sirota, S. Garoff, and H.B. Stanley, "X-ray and neutron scattering from rough surfaces", Phys. Rev. B, 38, 2297-2311, (1988).

 
Future Work
  • Development of sample Python scripts for automated access to X-Ray Server (in addition to already provided Perl and Bash scripts)
  • Development of interface to the X-Ray Server programs from the ESRF XOP package (collaboration with Manuel Sanchez del Rio).
  • Development of 4x faster version of GID_sl program
  • Implementation of the calculations of X-ray standing waves in the Bragg diffraction program (GID_sl)
  • Development of a new version of multiple diffraction program (BRL) which will be more stable numerically at arbitrary crystal thicknesses

 

Details

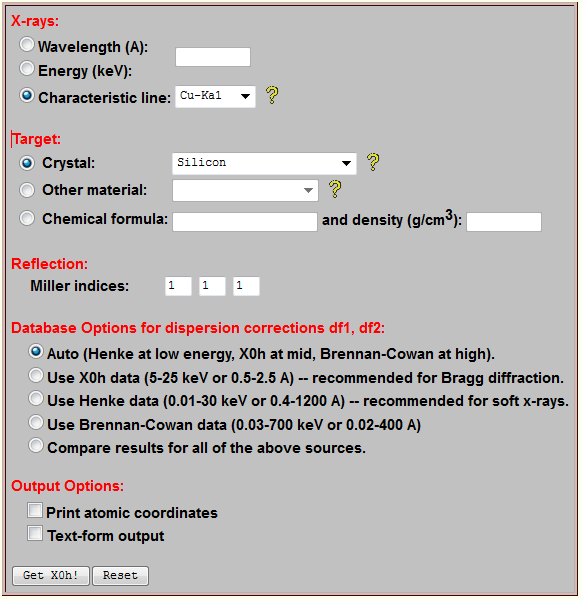
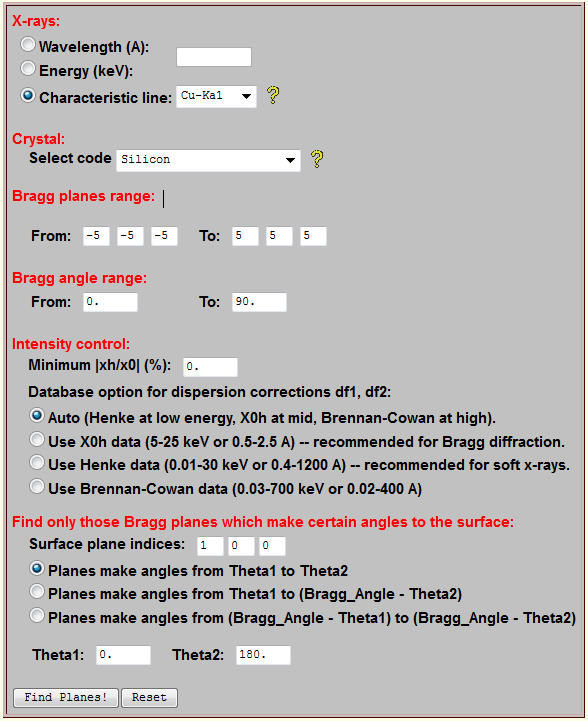
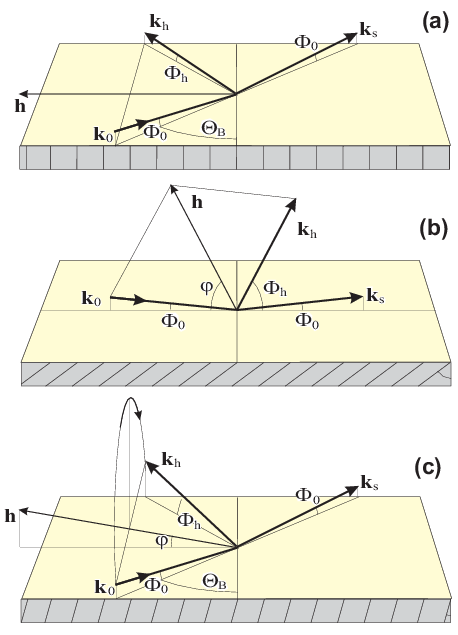
The programs accessible through X-Ray Server are outlined below.All examples on the Figures are taken from real users submissions as the results of all jobs are archived.For additional information and for program guides it is recommended to visit the respective programs pages at X-Ray Server.To facilitate quick learning, the programs are supplied with multiple versions of their input web forms, which are pre-filled for different usage scenarios.

 

Program X0h [implementing the algorithm from Lugovskaya & Stepanov, Sov. Phys. Crystallogr. 36, 478-481 (1991).], calculates scattering amplitudes for crystals and other materials in the X-ray range by interpolating tabulated data that are typically available for discrete wavelengths only.It also provides the associated values of the Bragg diffraction peak FWHM, extinction and absorption lengths and etc., which can be helpful in the analysis of diffraction experiments.The program has an option to compare the results based on three different sources of data.The database of crystals available with X0h is expandable per user submissions: a template is provided and more than a half of the structures are due to users.To obtain the results, one needs to fill a simple form in web browser, as shown on Fig.1.In addition to the web-browser access, X-Ray Server provides sample scripts demonstrating how to access X0h from user software and thus deploy it as a remote library.Finally, besides WWW interface, X0h supplies X-ray scattering factors to all other X-ray Server programs.  For example, when calculating a Bragg diffraction curve user only needs to specify a structure code from the X0h database.

 

Program X0h_search is an online tool based on X0h, which searches for Bragg planes in crystals under various conditions.It helps to find extremely asymmetric reflections in a crystal, strong reflections within certain Bragg angle range, Bragg planes making a range of angles with the surface, and etc.To obtain the results, user either needs to fill a simple form in web browser as shown on Fig.2 or tweak one of sample automation scripts.

 

Program GID_sl calculates X-ray Bragg diffraction rocking curves from perfect, strained and multilayered crystals, accounting for interface roughness for any Bragg-case geometry including out-of-plane cases, extremely asymmetric and grazing incidence diffraction (Fig.3a).Based on a series of papers [S.A. Stepanov, U. Pietsch and G.T. Baumbach,Zeitschrift für Physik B, 96, 341-347, (1995); S.A. Stepanov and R. Koehler,J. Appl. Phys. 76, 7809-7815, (1994); S.A. Stepanov and R. Koehler, J. Phys. D: Applied Physics, 27, 1923-1928, (1994); S.A. Stepanov, E.A. Kondrashkina, R. Koehler, D.V. Novikov, G. Materlik, and S.M. Durbin,  Phys. Rev. B, 57, 4829-4841, (1998)] it implements a combination of extended dynamical diffraction theory with due account for X-ray specular reflection and a recursive matrix algorithm to account for strain distributions over crystal depth and for diffraction from multilayers on top of crystal substrates.Some examples of what this program can do are shown on Fig.3b,c and more information is provided on the program home page.Having been used around 600,000 times, this is a well-refined software excelling some commercial rivals [see M. Grundmann and A. Krost, Phys. Status Solidi. (b), 218, 417–423, (2000).].The paper by Stepanov and Forrest [J.Appl.Cryst. 41, 958-962 (2008)] reports on using it for remote fitting of Bragg diffraction rocking curves from AlSb/AlAs superlattices.

 

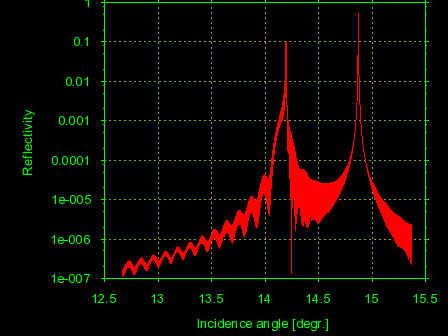
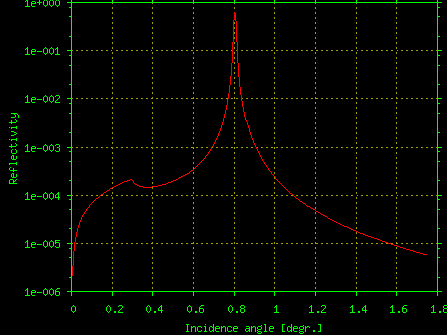
Program TER_sl calculates X-ray specular reflection and respective X-ray standing waves from X-ray mirrors and multilayers accounting for interface roughness or transition layers.  The method implemented in TER_sl is the same recursive matrix algorithm that was developed for the GID_sl program.  This method is neither Parratt's nor Abeles' and it is characterized by fast converging to the final curve while working from the surface down the multilayer stack.Some example of TER_sl results are shown on Fig.4.

 

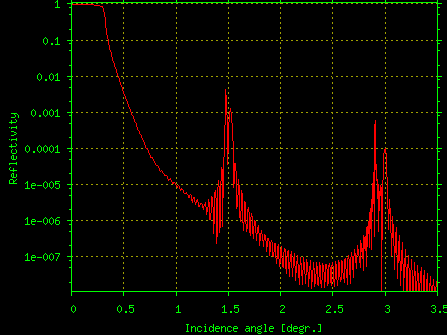
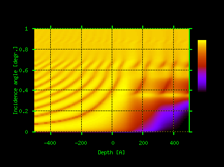
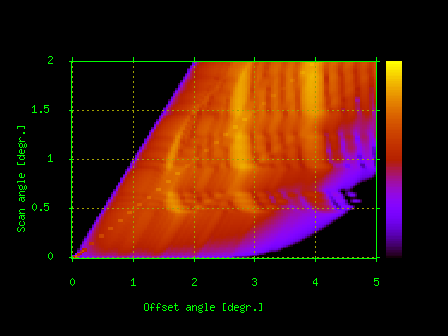
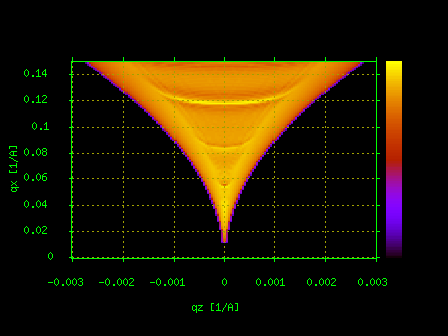
Program TRDS_sl calculates non-specular X-ray scattering from multilayers due to interface roughness.Studying surface and interface roughness using grazing-incidence X-ray is a powerful technique originating from the famous paper by Sinha et al. [Phys. Rev. B, 38, 2297-2311, (1988).].The angular pattern of non-specular scattering is related with the Fourier transform of roughness spectrum and therefore the measurements can provide the correlation function of statistical roughness distribution.TRDS_sl offers 10 different models of roughness and its propagation between interfaces.It can calculate such effects on X-ray scattering as the dependence of interface-interface roughness correlations in multilayers on the lateral roughness scale, skew roughness transfers in crystalline multilayers, scattering from atomic steps on vicinal surfaces, and etc.The program is based on papers [V.M. Kaganer, S.A. Stepanov and R. Koehler, Phys. Rev. B, 52, 16369-16372, (1995) and E.A. Kondrashkina, S.A. Stepanov, R. Opitz, M. Schmidbauer, R. Koehler, R. Hey, M. Wassermeier, and D.V. Novikov,Phys. Rev. B, 56, 10469-10482, (1997)] and also implements some models by other authors; see the TRDS_sl homepage for additional details and references.Multiple scan types are supported.Some examples of TRDS_sl results are shown on Fig.5.

 

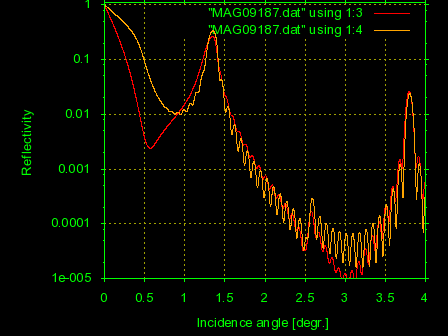
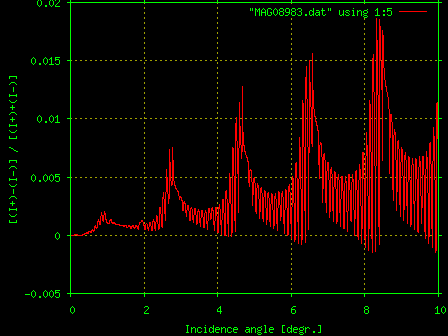
Program MAG_sl calculates resonant X-ray specular reflection from magnetic multilayers allowing for interface roughness or transition layers.It uses the equations derived in [S.A. Stepanov and S.K. Sinha, Phys. Rev. B, 61, 15302-15311, (2000) and D.R. Lee, S.K. Sinha, D. Haskel, Y. Choi, J.C. Lang, S.A. Stepanov, and G. Srajer,Phys. Rev. B, 68, 224409, (2003)].The effect it is calculating is a resonant increase in the electric multipole (e.g. quadrupole) part of X-ray scattering amplitude at the absorption edges of some rare-earth and transition elements.This effect makes the scattering amplitude a tensor with the orientation dependent on the orientation of the magnetic moment of respective atom.The X-ray scattering caused by this change in the scattering amplitude is called "resonant magnetic scattering", although it is electric by nature.When all the magnetic moments of atoms in the slab are oriented in the same direction, one can probe the magnetization of the media (e.g. thin magnetic film or magnetic multilayer) with X-rays.The effect on X-ray reflectivity is the strongest when the magnetic field is applied along the direction of X-ray grazing incidence and the incident X-rays are circularly polarized.Fig.6 shows some resonant specular reflectivity effects calculated with MAG_sl.

 

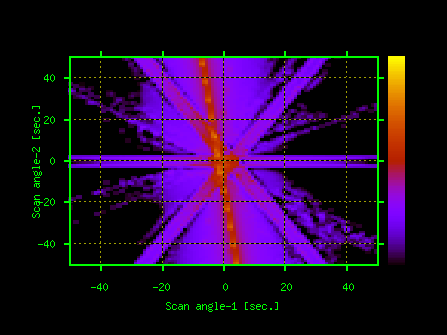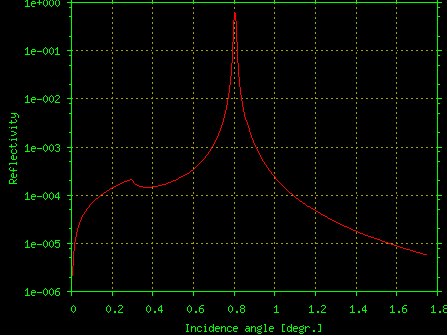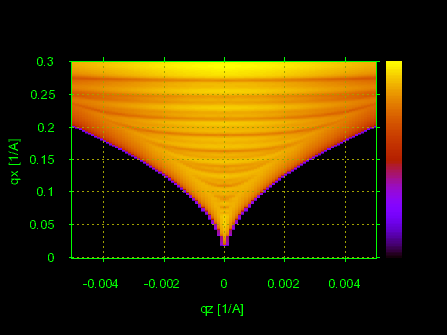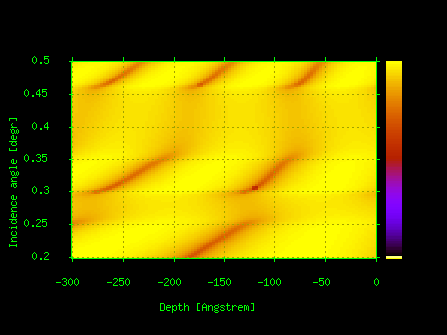
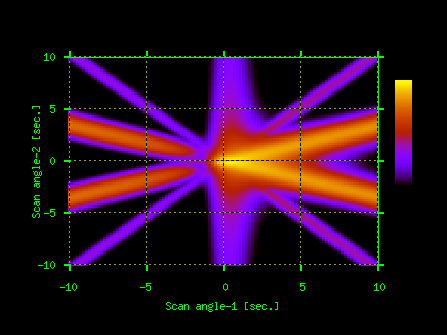
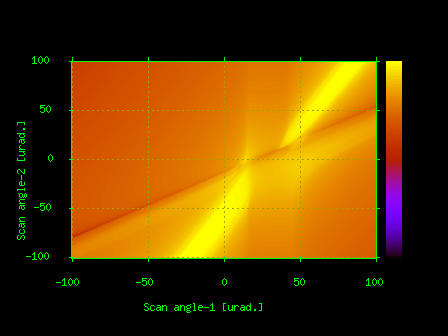
Program BRL calculates multiple Bragg diffraction of X-rays from crystals including cases with X-ray waves grazing along the crystal surface and Bragg angles close to 90 degrees.It is based on a paper by Stepanov and Ulyanenkov [Acta Cryst. A50, 579-585 (1994)] where the calculation of multiple Bragg diffraction was reduced to a generalized eigenvalue problem for 2(N+Ns)*2(N+Ns) scattering matrix where N is the number of reflections plus the incident wave and Ns is the number of grazing waves.BRL can calculate up to 12-wave dynamical Bragg diffraction of X-rays from a plate-shaped crystal.The program also helps to search for multiple Bragg diffraction conditions.One of possible applications of this program is evaluating multiple diffraction effects including the X-ray polarization state changes in synchrotron radiation X-ray monochromators.A few examples of BRL results are shown on Fig.7.