Ferromagnetic materials are key ingredients in vast arrays of technologies including wind turbines, computer hard-disks, credit card readers, and many more. Typically these magnets operate in moderate environments. But exposing a magnetic material to high heat or compressive stress usually destroys its magnetism because high temperatures and high compression induce agitation and mobility of unpaired electrons (“atomic compass”), destroying the correlated arrangement of atomic compasses across the solid needed to generate, or detect, magnetic fields. Scientists utilizing the U.S. Department of Energy Office of Science’s Advanced Photon Source (APS) at Argonne National Laboratory have found superb stability of ferromagnetism against compressive stress in an unconventional magnet.
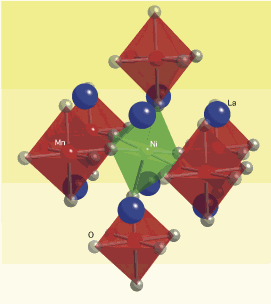
The researchers began investigating an unusual ferromagnetic oxide insulator composed of nickel, manganese, lanthanum, and oxygen atoms where electron mobility is limited. While most transition-metal monoxides do not possess net magnetization, an amusing ordering of Ni, Mn, and O atoms in this material (with a Ni-O-Mn-O-Ni-O-Mn, etc., ordering pattern) results in sizable net magnetization. As it turns out, this unconventional magnet is also extremely robust when subjected to compressive stress.
In a series of experiments, the Argonne scientists compressed the magnet between diamond anvils up to a pressure of 400,000 atmospheres while probing the materials’ magnetism and structure with x-ray absorption near edge structure and magnetic circular dichroism techniques at the X-ray Science Division 4-ID-D x-ray beamline, and powder x-ray diffraction at the High Pressure Collaborative Access Team 16-BM-D beamline, both at the APS.
Their results, published in the Rapid Communications section of Physical Review B showed that the magnetism remained unchanged within the few percent of experimental error. This is the first time that a ferromagnetic material has been found to retain its magnetic properties in such an extreme environment.
“Although we expected the unconventional ferromagnetism of this material to survive in a strained state, the superb stability exhibited under extreme stress conditions is a first, and totally surprising”, said the article’s lead author, Daniel Haskel. “This and other related complex oxide magnetic materials to be discovered should open opportunities for operation of magnets in environments not previously accessible.”
See: D. Haskel1*, G. Fabbris1,2, N. M. Souza-Neto3, M. van Veenendaal1,4, G. Shen5, A. E. Smith6, M. A. Subramanian6, “Stability of the ferromagnetic ground state of oxide insulator La2MnNiO6 against large compressive stress,” Phys. Rev. B 84, 100403 (2011).
DOI:10.1103/PhysRevB.84.100403
Author affiliations: 1Argonne National Laboratory, 2Washington University, 3Laboratorio Nacional de Luz Sincrotron-LNLS, 4Northern Illinois University, 5Carnegie Institution of Washington, 6Oregon State University
Correspondence: *[email protected]
Work at Argonne and NIU is supported by the U.S. Department of Energy, Office of Science, under contract Nos. DE-AC02-06CH11357 and DE-FG02-03ER46097, respectively. Work at Oregon State University is supported by NSF grant DMR0804167. HP-CAT is supported by CIW, CDAC, UNLV, LLNL through funding from DOE-NNSA, DOE-BES and NSF.
The Advanced Photon Source at Argonne National Laboratory is one of five national synchrotron radiation light sources supported by the U.S. Department of Energy’s Office of Science to carry out applied and basic research to understand, predict, and ultimately control matter and energy at the electronic, atomic, and molecular levels, provide the foundations for new energy technologies, and support DOE missions in energy, environment, and national security. To learn more about the Office of Science x-ray user facilities, visit http://science.energy.gov/user-facilities/basic-energy-sciences/.
Argonne National Laboratory seeks solutions to pressing national problems in science and technology. The nation's first national laboratory, Argonne conducts leading-edge basic and applied scientific research in virtually every scientific discipline. Argonne researchers work closely with researchers from hundreds of companies, universities, and federal, state and municipal agencies to help them solve their specific problems, advance America's scientific leadership and prepare the nation for a better future. With employees from more than 60 nations, Argonne is managed by UChicago Argonne, LLC for the U.S. Department of Energy's Office of Science.