Although materials scientists have theorized for years that a form of super-dense aluminum exists under the extreme pressures found inside a planet’s core, no one had ever actually seen it.
Until now, that is.
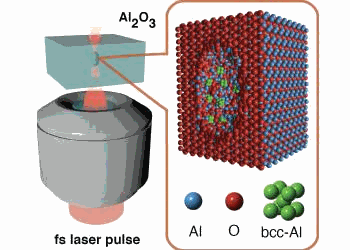
Using a new table-top laser device at Shizuoka University in Japan that penetrates crystals and sets off micro-explosions inside them, an international team of researchers blasted tiny bits of sapphire creating powerful shock waves that compressed the surrounding material. Under these extreme conditions—terapascals of pressure and temperatures of 100,000 Kelvin—warm dense matter forms, the state of matter between a solid and a plasma.
The researchers, from Stanford University, SLAC National Accelerator Laboratory, The Australian National University, Shizuoka University, Argonne National Laboratory, the Carnegie Institution of Washington, and Swinburne University of Technology then examined the interior of the sapphire, utilizing a beam of x-ray light from the High Pressure Collaborative Access Team (HP-CAT) beamline 16-BM-D at the U.S. Department of Energy Office of Science’s Advanced Photon Source at Argonne National Laboratory, and found a novel form of aluminum.
Because sapphire is a form of aluminum oxide, or alumina, the researchers expected to find evidence of various phases of high-pressure alumina inside the gem. Instead, they observed minuscule amounts of a surprisingly stable, highly-compressed form of elemental aluminum called body-centered cubic aluminum.
“High pressure experiments generally are done either with big equipment or with a diamond anvil cell where two diamonds are squeezing a tiny bit of material, but even diamond gives up at a certain point with those pressures,” said Arturas Vailionis, a researcher with the Geballe Laboratory for Advanced Materials and Stanford Institute for Materials & Energy Sciences and a co-author on the paper. “But this very short pulse of laser light actually ionizes all the material within a very small volume over a short time and creates a plasma which is under enormous pressure and temperature” without fracturing the outer shell of the sapphire.
Of particular interest is that the researchers “demonstrated that high-energy density produced in a simple tabletop experiment makes it possible to form an exotic high-density material phase which could not be produced by other means,” as noted in the nature communications paper.
While scientists long have predicted that new classes of materials with unusual combinations of physical properties should exist under extreme pressure and temperature conditions, only hcp-Al, the hexagonal close-packed aluminum phase, had been observed previously. The form made in this experiment is bcc-Al, or body-centered cubic aluminum.
Vailionis said he doesn’t expect the research to result in production of new materials in large quantities any time soon, but he believes the equipment used in the experiment offers a new strategy for synthesizing nanoscale amounts of new materials in the laboratory, and opens new possibilities for tabletop research into warm dense matter—the state of matter between a solid and a plasma. Such work could bring scientists a step closer to understanding Earth’s early history.
“Now we’re thinking about different materials we could use to recreate some of the environments that existed deep in the Earth’s core when the planet was forming,” he said.
See: Arturas Vailionis1,2, Eugene G. Gamaly3, Vygantas Mizeikis4, Wenge Yang5, Andrei V. Rode3, and Saulius Juodkazis6*, “Evidence of superdense aluminium synthesized by ultrafast microexplosion,” Nat. Commun. 2, 445 (23 August 2011). DOI: 10.1038/ncomms1449.
Author affiliations: 1Stanford University, 2SLAC National Accelerator Laboratory, 3The Australian National University, 4Shizuoka University, 5Carnegie Institution of Washington, 6Swinburne University of Technology
Correspondence: * [email protected]
This work was supported by the Australian Research Council through the Discovery program. HP-CAT is supported by the Carnegie Institution of Washington, the Carnegie-U.S. Department of Energy (DOE) Alliance Center, Lawrence Livermore National Laboratory, and the University of Nevada at Las Vegas through funding from the DOE-National Nuclear Security Administration, DOE-Basic Energy Sciences, and the National Science Foundation. HPSynC is supported as part of the EFree, an Energy Frontier Research Center funded by DOE-BES under award DE-SC000 1057.
Use of the Advanced Photon Source was supported by the DOE Office of Science under Contract No. DE-AC02-06CH11357).
The original SLAC News Center Feature story by Janet Rae-Dupree can be found here.
The Advanced Photon Source at Argonne National Laboratory is one of five national synchrotron radiation light sources supported by the U.S. Department of Energy’s Office of Science to carry out applied and basic research to understand, predict, and ultimately control matter and energy at the electronic, atomic, and molecular levels, provide the foundations for new energy technologies, and support DOE missions in energy, environment, and national security. To learn more about the Office of Science x-ray user facilities, visit http://science.energy.gov/user-facilities/basic-energy-sciences/.
Argonne National Laboratory seeks solutions to pressing national problems in science and technology. The nation's first national laboratory, Argonne conducts leading-edge basic and applied scientific research in virtually every scientific discipline. Argonne researchers work closely with researchers from hundreds of companies, universities, and federal, state and municipal agencies to help them solve their specific problems, advance America's scientific leadership and prepare the nation for a better future. With employees from more than 60 nations, Argonne is managed by UChicago Argonne, LLC for the U.S. Department of Energy's Office of Science.