000| Parameter Name | Units | Type | Default | Description |
| L | double | 0.0 | length | |
| XO | double | 0.0 | radiation length | |
| ELASTIC | long | 0 |
elastic scattering? If zero, then particles will lose energy due to material. | |
| ENERGY_STRAGGLE | long | 0 |
Use simple-minded energy straggling model? Ignored for ELASTIC scattering. | |
| Z | long | 0 |
Atomic number | |
| A | double | 0.0 | Atomic mass | |
| RHO | double | 0.0 | Density | |
| PLIMIT | double | 0.05 | Probability cutoff for each slice |
This element is based on section 3.3.1 of the Handbook of
Accelerator Physics and Engineering, specifically, the
subsections Single Coulomb scattering of spin-
![]() particles, Multiple Coulomb scattering through small angles,
and Radiation length.
There are two aspects to this element: scattering and energy loss.
particles, Multiple Coulomb scattering through small angles,
and Radiation length.
There are two aspects to this element: scattering and energy loss.
Scattering. The multiple Coulomb scattering formula is used
whenever the thickness of the material is greater than ![]() ,
where
,
where ![]() is the radiation length. (Note that this is inaccurate
for materials thicker than
is the radiation length. (Note that this is inaccurate
for materials thicker than ![]() .) For this regime, the user need
only specify the material thickness (L) and the radiation length (XO).
.) For this regime, the user need
only specify the material thickness (L) and the radiation length (XO).
For materials thinner than ![]() , the user must specify
additional parameters, namely, the atomic number (Z), atomic mass (A),
and mass density (RHO) of the material. Note that the density is
given in units of
, the user must specify
additional parameters, namely, the atomic number (Z), atomic mass (A),
and mass density (RHO) of the material. Note that the density is
given in units of ![]() . (Multiply by
. (Multiply by ![]() to convert
to convert ![]() to
to ![]() .) In addition, the simulation parameter PLIMIT may be
modified.
.) In addition, the simulation parameter PLIMIT may be
modified.
To understand this parameter, one must understand how elegant
simulates the thin materials. First, it computes the expected number
of scattering events per particle,
![]() , where
, where ![]() is the number density of
the material, L is the thickness of the material,
is the number density of
the material, L is the thickness of the material,
![]() , and
, and
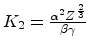 , with
, with ![]() the classical electron radius
and
the classical electron radius
and ![]() the fine structure constant. The material is then broken
into
the fine structure constant. The material is then broken
into ![]() slices, where
slices, where
![]() . For each slice, each
simulation particle has a probability
. For each slice, each
simulation particle has a probability ![]() of scattering. If scattering
occurs, the location within the slice is computed using a uniform
distribution over the slice thickness.
of scattering. If scattering
occurs, the location within the slice is computed using a uniform
distribution over the slice thickness.
For each scatter that occurs, the scattering angle, ![]() is
computed using the cumulative probability distribution
is
computed using the cumulative probability distribution
![]() . This can be solved for
. This can be solved for ![]() , giving
, giving
![]() . For each scatter,
. For each scatter,
![]() is chosen from a uniform random distribution on
is chosen from a uniform random distribution on ![]() .
.
Energy loss. Energy loss simulation is very simple.
The energy loss per unit distance traveled, ![]() , is
, is
![]() . Hence, in traveling through a
material of thickness
. Hence, in traveling through a
material of thickness ![]() , the energy of each particle is
transformed from
, the energy of each particle is
transformed from ![]() to
to ![]() .
.
Energy straggling. This refers to variation in the energy lost by particles. The model used by elegant is very, very crude. It assumes that the standard deviation of the energy loss is equal to half the mean energy loss. This is an overestimate, we think, and is provided to give an upper bound on the effects of energy straggling until a real model can be developed. Note one obvious problem with this: if you split a MATTER element of length L into two pieces of length L/2, the total energy loss will not not change, but the induced energy spread will be about 30% lower, due to addition in quadrature.